2016년06월18일 20번
[과목 구분 없음] α=48°, β=288°인 직선 와 직선 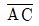 와 직선
와 직선 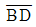 의 교차점은 P점이고 교차각 ∠APB가 θ일 때 cotθ의 값은?
의 교차점은 P점이고 교차각 ∠APB가 θ일 때 cotθ의 값은?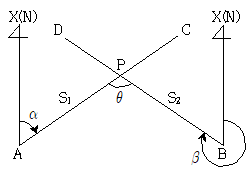
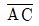 와 직선
와 직선 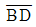 의 교차점은 P점이고 교차각 ∠APB가 θ일 때 cotθ의 값은?
의 교차점은 P점이고 교차각 ∠APB가 θ일 때 cotθ의 값은?
-
①
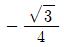
-
②
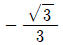
-
③
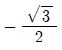
-
④
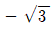
(정답률: 59%)
문제 해설
먼저 직선 l1과 l2의 교차점 P를 찾아보자.
각 α와 β는 각각 l1과 l2와 수직이므로, l1과 l2는 서로 수직이다.
따라서 P는 l1과 l2의 교차점이다.
다음으로 ∠APB를 구해보자.
∠APB는 두 직선의 교차각이므로,
∠APB = |α - β| = |48° - 288°| = 240°이다.
cotθ는 ∠APB의 보조각인 ∠CPD의 tan값과 같다.
∠CPD는 직선 l1과 l2에 의해 생기는 삼각형의 내각이므로,
∠CPD = 180° - ∠APB = 180° - 240° = -60°이다.
tan(-60°)은 tan(60°)과 같으므로,
cotθ = tan∠CPD = tan(-60°) = -√3이다.
따라서 정답은 "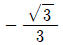 "이다.
"이다.
보기 설명:
"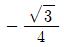 "은 ∠APB의 크기가 아닌, ∠CPD의 크기를 구하는 것이다.
"은 ∠APB의 크기가 아닌, ∠CPD의 크기를 구하는 것이다.
"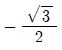 "은 ∠APB의 크기를 구하는 것이 아니라, ∠BPA의 크기를 구하는 것이다.
"은 ∠APB의 크기를 구하는 것이 아니라, ∠BPA의 크기를 구하는 것이다.
"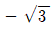 "은 cotθ의 값이 아니라 tanθ의 값이다.
"은 cotθ의 값이 아니라 tanθ의 값이다.
각 α와 β는 각각 l1과 l2와 수직이므로, l1과 l2는 서로 수직이다.
따라서 P는 l1과 l2의 교차점이다.
다음으로 ∠APB를 구해보자.
∠APB는 두 직선의 교차각이므로,
∠APB = |α - β| = |48° - 288°| = 240°이다.
cotθ는 ∠APB의 보조각인 ∠CPD의 tan값과 같다.
∠CPD는 직선 l1과 l2에 의해 생기는 삼각형의 내각이므로,
∠CPD = 180° - ∠APB = 180° - 240° = -60°이다.
tan(-60°)은 tan(60°)과 같으므로,
cotθ = tan∠CPD = tan(-60°) = -√3이다.
따라서 정답은 "
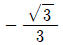 "이다.
"이다. 보기 설명:
"
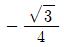 "은 ∠APB의 크기가 아닌, ∠CPD의 크기를 구하는 것이다.
"은 ∠APB의 크기가 아닌, ∠CPD의 크기를 구하는 것이다. "
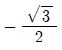 "은 ∠APB의 크기를 구하는 것이 아니라, ∠BPA의 크기를 구하는 것이다.
"은 ∠APB의 크기를 구하는 것이 아니라, ∠BPA의 크기를 구하는 것이다. "
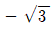 "은 cotθ의 값이 아니라 tanθ의 값이다.
"은 cotθ의 값이 아니라 tanθ의 값이다.
이전 문제
다음 문제



